币灵灵财经 2024-11-27 16:13 374
书接上回,关于《用多因子模型构建强大的加密资产投资组合》系列文章中,我们已经发布了四篇:《理论基础篇》、《数据预处理篇》、《因子有效性检验篇》、《大类因子分析:因子合成篇》。
在上一篇中,我们具体解释了因子共线性(因子之间相关性较高)的问题,在进行大类因子合成前,需要进行因子正交化来消除共线性。

从多因子截面回归角度,建立因子正交化体系。

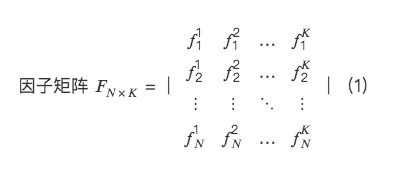

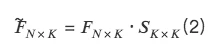

所以,
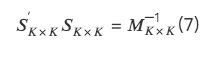



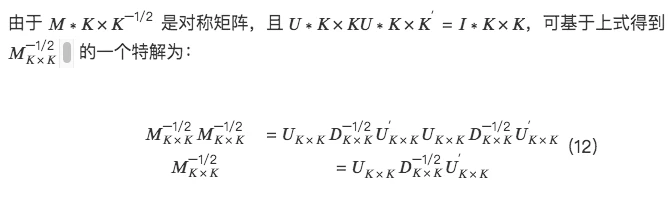







施密特正交是一种顺序正交方法,因此需要确定因子正交的顺序,常见的正交顺序有固定顺序(不同截面上取同样的正交次序),以及动态顺序(在每个截面上根据一定规则确定其正交次序)。施密特正交法的优点是按同样顺序正交的因子有显式的对应关系,但是正交顺序没有统一的选择标准,正交后的表现可能受到正交顺序标准和窗口期参数的影响。


 # 规范正交 def Canonical(self): overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float)) # 获取特征值和特征向量 eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix) # 转换为 np 中的矩阵 eigenvector = np.mat(eigenvector) transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5)))) orthogonalization = np.dot(time_tag_data.T.values, transition_matrix) orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns) self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)
# 规范正交 def Canonical(self): overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float)) # 获取特征值和特征向量 eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix) # 转换为 np 中的矩阵 eigenvector = np.mat(eigenvector) transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5)))) orthogonalization = np.dot(time_tag_data.T.values, transition_matrix) orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns) self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)
施密特正交由于在过去若干个截面上都取同样的因子正交顺序,因此正交后的因子和原始因子有显式的对应关系,而规范正交在每个截面上选取的主成分方向可能不一致,导致正交前后的因子没有稳定的对应关系。由此可见,正交后组合的效果,很大一部分取决于正交前后因子是否有稳定的对应关系。
对称正交尽可能的减少对原始因子矩阵的修改而得到一组正交基。这样能够最大程度地保持正交后因子和原因子的相似性。并且避免像施密特正交法中偏向正交顺序中靠前的因子。

对称正交的性质:
与施密特正交相比,对称正交不需要提供正交次序,对每个因子是平等看待的
在所有正交过渡矩阵中,对称正交后的矩阵和原始矩阵的相似性最大,即正交前后矩阵的距离最小。

热门文章
为华为手机提供摄像头模组?欧菲光董事长回应
萨尔瓦多比特币浮盈8300万美元!Tim Draper:将成最富裕国家之一
大模型独角兽“智谱 AI”正以200亿元估值进行新一轮融资,此前阿里腾讯等已投资25亿
跨境理财通2.0正式起航 个人投资者额度提高到300万元
9月8日涨停复盘:捷荣技术8天7板 华映科技7天6板
又一城缩减住宅限购范围!已有7个省会城市全面取消限购
Voyager赔偿用户需再等!清算计划修正版待法院批准才能分配代币
5.24 是多还是空 我们该如何抉择?
3年内禁止参加军队采购!奥维通信围标串标被罚 影响几何?
未来健康获罗斯柴尔德家族1亿美金投资,与国际NMN医药集团合作打造全球首创NMN期货产品